Learning Stochastic Differential Equations With Gaussian Processes Without Gradient Matching
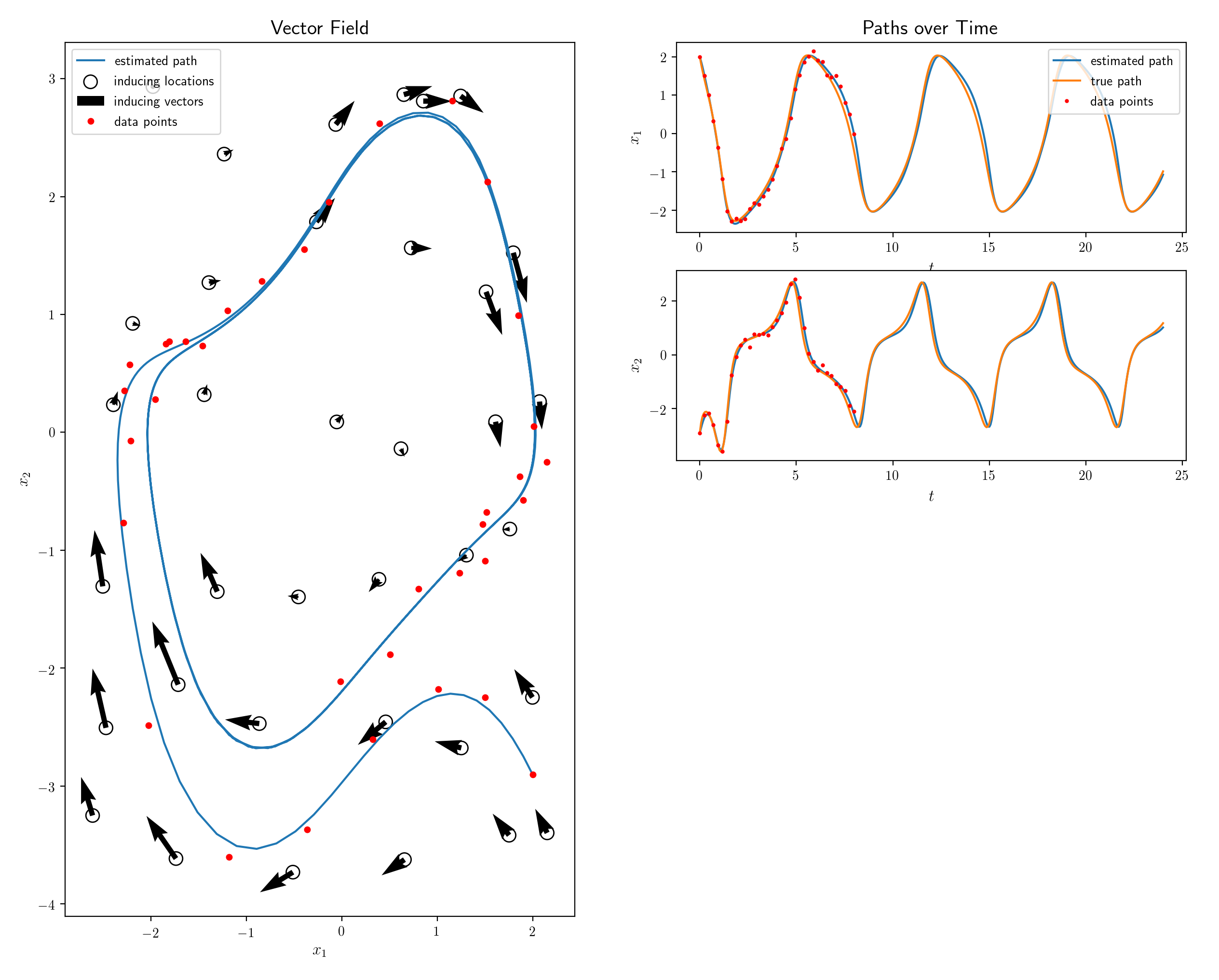
We introduce a novel paradigm for learning non-parametric drift and diffusion functions for stochastic differential equation (SDE). The proposed model learns to simulate path distributions that match observations with non-uniform time increments and arbitrary sparseness, which is in contrast with gradient matching that does not optimize simulated responses. We formulate sensitivity equations for learning and demonstrate that our general stochastic distribution optimisation leads to robust and efficient learning of SDE systems.
PDF AbstractCode
Tasks
Datasets
Add Datasets
introduced or used in this paper
Results from the Paper
Submit
results from this paper
to get state-of-the-art GitHub badges and help the
community compare results to other papers.
Methods
No methods listed for this paper. Add
relevant methods here